Исследование влияния геометрии сферодина на метод сферодинамического формообразования деталей агрегатов изделий ракетно-космической техники

УДК 621.983:514.113.6

Исследование влияния геометрии сферодина на метод сферодинамического формообразования деталей агрегатов изделий ракетно-космической техники

A Study of the Spherodyne Geometry Influence on the Spherodynamic Shaping Method of the Aerospace Equipment Assembly Parts

Введение

Эффект сферодинамики (далее – эффект) открыт при запуске пресса сферодвижной обкатки мод. PXW-100 (Р=1,6 кН, Польша), когда из-за потери фирменных выталкивателей (опор цилиндрических заготовок в полости матрицы) использовались выталкиватели из других материалов, что привело к периодическим разрушениям выталкивателей в зоне их контакта с заготовкой [1].

Для решения проблемы предлагалось обработать профиль рабочей поверхности пуансона и выполнить составным выталкиватель с профильными частями различной геометрии со стороны заготовки. При опытной отработке штамповки установлено, что при внесении деформации в материал от торцев заготовки по траектории в форме логарифмической спирали Бернулли с шагом роста, находящимся в пределах изменения высотной степени деформации материала заготовки в условиях реализации эффекта Баушингера [2] («запоминание» материалом истории его нагружения) (обозначим спираль – спираль Баушингера), верхняя часть выталкивателя (сферодин) периодически нарушает свои первоначальные гравитационные условия (левитирует) и автономно (без привода) обрабатывает нижний торец заготовки в режиме хаотических биений.

При этом установлено, что сферодин обеспечивает наибольшую степень изменения исходной структуры материала заготовки. Однако указанный феномен левитирования сферодина не регламентирован во времени его возникновения и развития.

Экспериментальные исследования выявили наличие признаков в форме элементов сферосистемы (пуансон – заготовка – сферодин – выталкиватель – матрица) и в траектории их перемещения, признаки, имеющие геометрию, схожую со спиралью Баушингера, и являющиеся определяющим фактором возникновения и реализации эффекта.

На основании этого установлено: увеличение суммарной спиральности, вносимой в сферосистему на начальных стадиях реализации эффекта, прямым образом определяет момент и длительность левитирования сферодина, а также характер и степень изменения структуры обрабатываемого материала заготовки.

Сферодинамическая система относится к нелинейным динамическим системам, поскольку свойства материала заготовки изменяются в процессе её деформирования.

Теоретические исследования природы возникновения спонтанных хаотических движений отдельных элементов нелинейных динамических систем [3], а также теории вихрей в различных средах [4] выявили, что при свободном вращении твёрдого тела с полостью, частично заполненной жидкостью, находящегося в зоне вращающихся постоянных магнитов, момент спонтанного перехода вращения тела к хаотическому движению по сравнению с вращающимся монолитным телом той же формы (в отсутствии постоянных магнитов), наступает значительно раньше. Таким образом, при разработке оптимальной конструкции сферодина на основании данных экспериментальных и теоретических исследований руководствовались следующим положением: обеспечить максимально возможное внесение суммарной спиральности с геометрией спирали Баушингера в сферосистему на первых стадиях реализации эффекта, что обусловило бы в процессе работы сферосистемы одновременное возникновение спиральных полей вращения постоянных магнитов, жидких сред и, как результат, формирование единообразного спирального перемещения всех подвижных элементов сферосистемы.

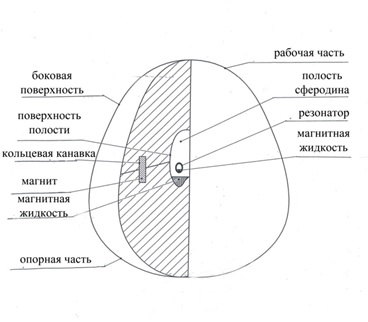
Итогом проведённых исследований явилась разработка конструкции сферодина (рис. 1), выполненной в форме «яйцевидного» тела, образованного вращением бóльшей половины витка логарифмической спирали ЛС1 вокруг бóльшей оси; с формой полости, образованной вращением бóльшей половины витка логарифмической спираль ЛС2 вокруг бóльшей оси, частично заполненной магнитной жидкостью и содержащей полную твёрдую сферу (резонатор), также частично заполненную магнитной жидкостью, с внутренней кольцевой выемкой, в которой размещены постоянные магниты с зазорами между собой, изменяющимися по кривой в форме логарифмической спирали ЛС3.

Рис. 1. Сферодин

Необходимо отметить, что все три спиральных элемента ЛС1, ЛС2, ЛС3 сферодина, как и спиральный профиль рабочей поверхности пуансона, выполнены по геометрии спирали Баушингера, что позволяет регламентировано формировать однотипные спиральные элементы по ходу реализации эффекта:

• спиральные поля вращений постоянных магнитов и магнитных жидкостей (два механизма «турбулентного вихревого динамо» ТВД1, ТВД2);
• встречное перемещение очагов деформации от пуансона и сферодина в материале заготовки по спиральным «шнурам» локализации деформации.

Согласно принципу геометрического подобия причинно-следственной связи формируемых объектов [5] – геометрия причины определяет геометрию следствия – происходит следующее: в обрабатываемый материал заготовки вносится семейство однотипных спиральных элементов и, одновременно с этим, в окружающую заготовку воздушную среду (вращение постоянных магнитов сферодина). При этом материал заготовки согласно эффекту Баушингера накапливает вносимые возмущения по законам спиральной симметрии, фундаментальным свойствам которой является т.н. «цепляемость» логарифмических спиралей [5], что обуславливает непрерывный реверсивный обмен энергией между тремя средами: «магнитные жидкости сферодина» –  (встречнонаправленные спиральные «шнуры» очагов деформации в заготовке от пуансона и сферодина) – газообразная среда (спиральные поля вращения постоянных магнитов сферодина в воздушном пространстве динамической части сферосистемы «пуансон – заготовка – сферодин»). Таким образом, перед левитированием сферодина в сферосистеме формируется единая спиральная пространственная система в трёх различных средах в зоне взаимодействия трёх элементов: «пуансон – заготовка – сферодин».

Согласно эндохронной теории пластичности (ЭТП) [6] К. Валанис предложил единую меру внутреннего времени, создаваемую приводным инструментом в деформируемом теле. Наличие в сферосистеме сферодина как бесприводного источника реактивного деформирования формирует в деформируемой заготовке два встречнонаправленных потока: СВВ₁ – сферодинамическое внутреннее время от пуансона (активное) и СВВ₂ – соответственно от сферодина (реактивное). При этом природа СВВ₂ принципиально отличается от общепринятой [6], поскольку является вторичной реакцией среды на вносимое в неё возмущение, т.е. деформируемая среда со стороны сферодина сама является импульсом возмущения.

Таким образом, на стадии левитирования сферодина в сферосистеме одновременно присутствуют две физические категории:

• единая спиральная пространственная система в трёх различных средах: «жидкость – твёрдое тело – газ» в зоне взаимодействия трёх элементов «пуансон – заготовка – сферодин»;
• встречнонаправленные потоки различных внутренних времен в деформируемой заготовке, также спиральной пространственной конфигурации.

Эти физические категории формируют новую физическую категорию: сферодинамический пространственно-временной континуум (материальная среда, свойства которой изменяются в пространстве непрерывно).

Сферодинамическая система относится к нелинейным динамическим системам, в которых периодически создаётся ситуация возникновения и проявления детерминированного хаоса. Теория беспорядка (хаоса) предполагает возможность существования пространственно неупорядоченных распределений некоторых физических категорий до конца пока не регламентированных, одной из которых является случайное поле. Существование случайных полей предсказано А. Колмогоровым и определено как полевая форма материи, создаваемая семейством случайных функций, являющихся следствием развития в пространстве динамики инвариантных спиралей Винера, Бернулли [5].

Установлено, что для нелинейных динамических систем, а в данном случае для сферосистемы переход от квазипериодичности (деформационный резонанс сферосистемы) к конечному пространственному беспорядку (левитирование сферодина) является следствием образования нового пространственно-временного континуума, сформированного гаммой случайных полей, неподдающихся регламентации во времени, однако формирующих спиральность этого континуума на основании причинно-следственного подобия.

Таким образом, геометрия сферодина в форме тела вращения элемента логарифмической спирали Баушингера определена при устранении спонтанного возникновения неконтролируемых аномальных растягивающих напряжений в зоне контакта заготовки с выталкивателем при известных методах сферодвижной обработки. С другой стороны, геометрия сферодина приобрела роль методологического инструмента, определяющего:

• геометрию всех элементов сферодинамической системы, реализующих эффект сферодинамики и вносящих возмущение в деформируемое твёрдое тело и окружающее его пространство;
• геометрию динамики пространственного развития возмущений в системе трёх контактирующих сред «жидкость – твёрдое тело – газ»;
• геометрию формируемых «внутренних времён» в упомянутых возмущённых средах;
• геометрию выхода на полевой уровень этих возмущений за счёт т.п. «цепляемости» возмущений в виде разномасштабных логарифмических спиралей, образующих гамму случайных полей, следствие развития которых явилось формирование новой физической категории – сферодинамического пространственно-временного континуума, временно изменяющего первоначальные гравитационные условия сферодина;
• геометрию всех структурных компонент материала твёрдого тела после сферодинамической обработки.

Установленное «сквозное» спиральное единообразие геометрии элементов сферосистемы и геометрии её «жизненного цикла» при реализации эффекта сферодинамики, позволяет обозначить пространственно-временные контуры ещё не изученного свойства материи, характеризующего «динамику спирального масштабирования распространения возмущения в материальной среде».

Выводы

1. Определено значение геометрии сферодина как методологического инструмента при реализации эффекта сферодинамики.
2. Выявлена разномасштабность динамики развития возмущений в пространственно-временных условиях развития эффекта.

Библиографический список

1. Бещеков В.Г. Сферодинамика т. 1. – М.: Научный мир, 2018. – 499 с.
2. Выгодский М.Я. Справочник по высшей математике. – М.: Наука, 1976. – 870 с.
3. Белов А.Н. Нелинейные динамические системы. – М.: Наука, 1985. – 263 с.
4. Пригожин И.А. Теория вихрей. – М.: Наука, 1988. – 425 с.
5. Колмогоров А.Н. Теория случайных полей. – М.: Наука, 1966. – 127 с.
6. Быков Д.Л. Нелинейная эндохронная теория стареющих вязкоупругих материалов // Механика твёрдого тела. – 2002. – № 4. – С. 63-76.

Бещеков Владимир Глебович – докт. техн. наук, главный научный сотрудник ФГУП «НПО «Техномаш» им. С.А. Афанасьева. Тел.: 8(495)689-95-10. E-mail: 130-110@tmnpo.ru / Beshchekov Vladimir Glebovich – Doktor Nauk in Engineering, Principal Research Officer of FSUE «NPO «Technomac» named after S.A. Afanasev.Tel.: 8(495)689-95-10. E-mail: 130-110@tmnpo.ru

Синякова Татьяна Ивановна – инженер-технолог 1 категории, ФГУП «НПО «Техномаш» им. С.А. Афанасьева. Тел.: 8(495)689-95-10. E-mail: 130-110@tmnpo.ru / Siniakova Tatiana Ivanovna – Category 1 Process Engineer of FSUE «NPO «Technomac» named after S.A. Afanasev. Tel.: 8(495)689-95-10. E-mail: 130-110@tmnpo.ru

Бочаров Юрий Андреевич – инженер-технолог 1 категории, ФГУП «НПО «Техномаш» им. С.А. Афанасьева. Тел.: 8(495)689-95-10. E-mail: 130-110@tmnpo.ru / Bocharov Iurii Andreevich – Category 1 Process Engineer of FSUE «NPO «Technomac» named after S.A. Afanasev. Tel.: 8(495)689-95-10. E-mail: 130-110@tmnpo.ru